Ora è giunto il momento di fare un piccolo balzo in avanti, andando a scoprire gli strumenti basilari dell'analisi complessa.
Tralasceremo nella narrazione di questo articolo (e di quelli che seguiranno sull'argomento) molte dimostrazioni e tecnicismi esagerati; lo scopo primario qui è infatti di rendere accessibili e digeribili ad un lettore, con un minimo bagaglio di conoscenze dell'analisi matematica reale, le interessanti nozioni fondamentali dell'analisi complessa.
Diciamo innanzitutto che la parte dell'analisi matematica che si occupa dello studio delle funzioni di variabili complesse è generalmente chiamata teoria delle funzioni analitiche.
Premesso che una funzione è analitica nelle regioni dove essa è perfettamente definita (continua con tutte le sue derivate), la teoria delle funzioni analitiche è rivolta, in verità, specialmente allo studio dei punti (o delle regioni) di non analiticità delle funzioni stesse, essendo proprio tali punti, i cosiddetti punti singolari, quelli che determinano le caratteristiche fondamentali delle funzioni considerate.
Le uniche "funzioni" ovunque analitiche sono infatti banalmente costanti.
Una variabile complessa

vien detta funzione della variabile complessa
se esiste una corrispondenza prefissata fra i valori di z e quelli di w; se cioè ad ogni valore di z (fissato in modo qualsiasi in un certo insieme) corrispondono uno o più valori di w.
Nel primo caso la funzione sarà detta monodroma (o a un solo valore), nel secondo polidroma.
Ciò equivale a dire, in pratica, che le 2 funzioni u e v sono funzioni reali delle 2 variabili x e y.
Lo studio delle funzioni di una variabile complessa sembra quindi, a prima vista, potersi ricondurre a quello delle funzioni reali di 2 variabili reali.
In verità, le funzioni analitiche soddisfano a particolari condizioni restrittive che fan sì che queste godano di proprietà peculiari e possano essere studiate direttamente come funzioni di una variabile (complessa).
I concetti basilari della teoria delle funzioni di una variabile reale, come limite e continuità, risultano facilmente estendibili ad una generica funzione di variabile complessa
In tal modo, supposto che f(z) sia definita sui punti di un insieme E e che z₀ ∈ E sia un punto di accumulazione (limite) di E, diremo che f(z) tende ad un limite l per z → z₀ se, fissato un numero positivo ε arbitrario (piccolo quanto si vuole), è possibile trovare un numero positivo δ tale che:

con

Se una funzione f(z) è definita su un insieme continuo C di valori di z, essa risulta continua nel punto z₀ ∈ C se esiste ed è finito il limite di f(z) per z → z₀ e questo limite coincide con f(z₀).
Una sostanziale difficoltà si incontra invece quando si cerca di estendere alle funzioni di variabile complessa (in generale) il concetto di derivata.
La derivata di una funzione di variabile complessa non è infatti definita sempre in modo univoco.
Tuttavia le funzioni di maggiore rilevanza, ossia le funzioni analitiche, sono proprio quelle per cui la derivata è definita in maniera univoca.
Diciamo ora che f(z) è derivabile in senso complesso (o anche che f è olomorfa) in z₀ ∈ D, con D insieme di definizione di f(z), se esiste, finito, il limite del rapporto incrementale quando z → z₀.
Tale limite si indicherà con f'(z₀) e verrà detto derivata di f in z₀.
In simboli:
La definizione è apparentemente "innocua", ma, come anticipato, è molto più restrittiva di quanto possa sembrare a prima vista.
Essa richiede infatti che il limite del rapporto incrementale esista e sia lo stesso quale che sia il modo (la velocità, come grandezza vettoriale) con cui z tende a z₀.
Tutto ciò impone condizioni severe sulle derivate parziali delle funzioni u(x, y) e v(x, y).
Sussiste il seguente teorema fondamentale:
"Condizione necessaria e sufficiente per la derivabilità di f(z) nel punto z₀ ∈ D è che le funzioni u(x, y) e v(x, y) siano differenziabili in (x₀, y₀) e le loro derivate parziali prime obbediscano alle ≪condizioni di Cauchy-Riemann≫:

"
Le condizioni di Cauchy-Riemann, "marchio di fabbrica" delle funzioni analitiche, prendono la denominazione da Augustin-Louis Cauchy, che fu il primo ad utilizzarle nell'ambito dell'analisi complessa, e da Riemann, che le rese fondamentali nel proprio sviluppo della teoria delle funzioni analitiche, avvenuto nella sua tesi del 1851.
In realtà, tali equazioni vennero utilizzate per la primissima volta da d'Alembert nel 1752.
A volte si trovano pure scritte nella forma:

Derivando le condizioni di Cauchy-Riemann in ∂x e ∂y rispettivamente, si ha:
ergo:

Il 1° membro della suddetta equazione è chiaramente il laplaciano (ne abbiamo parlato qui) di u, ossia ∇²u.
Le funzioni tali che ∇²u = 0 si dicono funzioni armoniche.
Se f = u + iv è olomorfa, u risulta armonica.
Similmente si verifica che anche v è armonica, ovvero che

L'equazione

è denominata equazione di Laplace e costituisce un primo esempio di equazione differenziale alle derivate parziali.
Due funzioni u e v legate tra loro dalle condizioni di Cauchy-Riemann vengono poi chiamate coniugate.
Entriamo ora un po' più nello specifico nella definizione delle funzioni analitiche.
Una funzione w = f(z) è analitica regolare o olomorfa (o anche monogena) in un punto z = z₀ se f(z) è definita e continua per z = z₀ e ivi derivabile in modo univoco (più precisamente, se la funzione è olomorfa in qualche intorno del punto z₀).
Le condizioni di Cauchy-Riemann sono quindi le condizioni cui deve soddisfare una funzione di variabile complessa affinché sia analitica in un generico punto z.
Una funzione è poi olomorfa (o regolare) in tutta una regione se in qualsiasi punto di tale regione le condizioni di Cauchy-Riemann risultano soddisfatte.
In tutta la regione, f(z) sarà allora dotata di derivata prima f'(z) unica e (come mostrato da Edouard Goursat) variabile con continuità al variare di z.
Se viceversa in un punto z = z₀ non esiste una derivata unica di f(z) (o, addirittura, la funzione stessa non è lì continua o definita in maniera univoca) si dice che il punto z = z₀ è un punto singolare della funzione f(z).
Va constatato che nella regione di olomorfismo di una funzione di variabile complessa valgono le ordinarie regole del calcolo differenziabile.
Vediamo un semplice esempio di funzione analitica:

Questa è analitica in tutto il campo |z| < ∞.
Infatti si ha:

Le derivate parziali prime sono:


e soddisfano alle condizioni di olomorfismo di Cauchy-Riemann per qualsiasi valore finito di z.
Si ha allora univocamente
Il punto z = ∞ va escluso dalla regione di olomorfismo in quanto la funzione stessa z² non è lì definita (risulta cioè infinita) e lo stesso accade per la sua derivata.
È interessante osservare adesso un esempio di funzione non analitica:
ove z* è il complesso coniugato di z.
Vediamo infatti che
e pur valendo la condizione
risulta però

Ergo, la prima delle condizioni di Cauchy-Riemann non è soddisfatta.
Pur essendo z* una funzione di z perfettamente definita, non ha alcun senso parlare della sua derivata fatta rispetto a z.
Possiamo concludere che l'operazione di coniugazione complessa non è un'≪operazione analitica≫.
Ultima osservazione: somma (e differenza) e prodotto di 2 funzioni analitiche sono ancora funzioni analitiche nella regione intersezione delle regioni di olomorfismo delle 2 funzioni date.
Per il momento ci fermiamo qui; la prossima volta incominceremo a introdurre l'integrazione complessa, un argomento lungo e articolato.

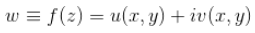

























Nessun commento:
Posta un commento